EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 15 / No 4 (October-December 2009) ESAIM: COCV, 15 4 (2009) 914-933 References
Free Access
Issue
ESAIM: COCV
Volume 15, Number 4, October-December 2009
Page(s) 914 - 933
DOI https://doi.org/10.1051/cocv:2008058
Published online 20 August 2008
  1. F. Alessio, L. Jeanjean and P. Montecchiari, Existence of infinitely many stationary layered solutions in 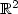Formula for a class of periodic Allen-Cahn equations. Comm. Partial Diff. Eq. 27 (2002) 1537–1574. [Google Scholar]
  2. S. Allen and J. Cahn, A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27 (1979) 1084–1095. [Google Scholar]
  3. A. Ambrosetti and M. Badiale, Homoclinics: Poincaré-Melnikov type results via a variational approach. Ann. Inst. H. Poincaré Anal. Non Linéaire 15 (1998) 233–252. [CrossRef] [MathSciNet] [Google Scholar]
  4. D.I. Borisov, On the spectrum of the Schrödinger operator perturbed by a rapidly oscillating potential. J. Math. Sci. (N. Y.) 139 (2006) 6243–6322. [CrossRef] [MathSciNet] [Google Scholar]
  5. H. Brezis, Analyse fonctionnelle. Théorie et applications. Collection Mathématiques Appliquées pour la Maîtrise, Masson, Paris (1983). [Google Scholar]
  6. G. Carbou, Unicité et minimalité des solutions d'une équation de Ginzburg-Landau. Ann. Inst. H. Poincaré Anal. Non Linéaire 12 (1995) 305–318. [Google Scholar]
  7. R. de la Llave and E. Valdinoci, Multiplicity results for interfaces of Ginzburg-Landau-Allen-Cahn equations in periodic media. Adv. Math. 215 (2007) 379–426. [CrossRef] [MathSciNet] [Google Scholar]
  8. N. Dirr and E. Orlandi, Sharp-interface limit of a Ginzburg-Landau functional with a random external field. Preprint, http://www.mat.uniroma3.it/users/orlandi/pubb.html (2007). [Google Scholar]
  9. N. Dirr and N.K. Yip, Pinning and de-pinning phenomena in front propagation in heterogeneous media. Interfaces Free Bound. 8 (2006) 79–109. [CrossRef] [MathSciNet] [Google Scholar]
  10. N. Dirr, M. Lucia and M. Novaga, Formula -convergence of the Allen-Cahn energy with an oscillating forcing term. Interfaces Free Bound. 8 (2006) 47–78. [CrossRef] [MathSciNet] [Google Scholar]
  11. L.C. Evans, Partial differential equations, Graduate Studies in Mathematics 19. American Mathematical Society, Providence, RI (1998). [Google Scholar]
  12. A. Farina and E. Valdinoci, Geometry of quasiminimal phase transitions. Calc. Var. Partial Differential Equations 33 (2008) 1–35. [CrossRef] [MathSciNet] [Google Scholar]
  13. G. Gallavotti, The elements of mechanics, Texts and Monographs in Physics. Springer-Verlag, New York (1983). Translated from the Italian. [Google Scholar]
  14. D. Gilbarg and N.S. Trudinger, Elliptic partial differential equations of second order, Grundlehren der Mathematischen Wissenschaften 224. Springer-Verlag, Berlin, second edition (1983). [Google Scholar]
  15. V.L. Ginzburg and L.P. Pitaevskiĭ, On the theory of superfluidity. Soviet Physics. JETP 34 (1958) 858–861 (Ž. Eksper. Teoret. Fiz. 1240–1245). [MathSciNet] [Google Scholar]
  16. T. Kato, Perturbation Theory for Linear Operators, Classics in Mathematics. Springer-Verlag, Berlin (1995). [Google Scholar]
  17. L.D. Landau, Collected papers of L.D. Landau. Edited and with an introduction by D. ter Haar, Second edition, Gordon and Breach Science Publishers, New York (1967). [Google Scholar]
  18. M. Marx, On the eigenvalues for slowly varying perturbations of a periodic Schrödinger operator. Asymptot. Anal. 48 (2006) 295–357. [MathSciNet] [Google Scholar]
  19. V.K. Mel'nikov, On the stability of a center for time-periodic perturbations. Trudy Moskov. Mat. Obšč. 12 (1963) 3–52. [MathSciNet] [Google Scholar]
  20. H. Matano and P.H. Rabinowitz, On the necessity of gaps. J. Eur. Math. Soc. (JEMS) 8 (2006) 355–373. [CrossRef] [MathSciNet] [Google Scholar]
  21. M. Novaga and E. Valdinoci, The geometry of mesoscopic phase transition interfaces. Discrete Contin. Dyn. Syst. 19 (2007) 777–798. [CrossRef] [MathSciNet] [Google Scholar]
  22. H. Poincaré, Les méthodes nouvelles de la mécanique céleste. Gauthier-Villars, Paris (1892). [Google Scholar]
  23. P.H. Rabinowitz and E. Stredulinsky, Mixed states for an Allen-Cahn type equation. Comm. Pure Appl. Math. 56 (2003) 1078–1134. Dedicated to the memory of Jürgen K. Moser. [Google Scholar]
  24. P.H. Rabinowitz and E. Stredulinsky, Mixed states for an Allen-Cahn type equation. II. Calc. Var. Partial Diff. Eq. 21 (2004) 157–207. [Google Scholar]
  25. J.S. Rowlinson, Translation of J.D. van der Waals' “The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density”. J. Statist. Phys. 20 (1979) 197–244. [Google Scholar]
  26. M. Schatzman, On the stability of the saddle solution of Allen-Cahn's equation. Proc. Roy. Soc. Edinburgh Sect. A 125 (1995) 1241–1275. [MathSciNet] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.