EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 11 / No 4 (October 2005) ESAIM: COCV, 11 4 (2005) 633-672 References
Free Access
Issue
ESAIM: COCV
Volume 11, Number 4, October 2005
Page(s) 633 - 672
DOI https://doi.org/10.1051/cocv:2005023
Published online 15 September 2005
  1. S. Alama, L. Bronsard and C. Gui, Stationary layered solutions in 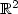Formula for an Allen-Cahn system with multiple well potential. Calc. Var. 5 (1997) 359–390. [Google Scholar]
  2. G. Alberti, L. Ambrosio and X. Cabré, On a long-standing conjecture of E. De Giorgi: Symmetry in 3D for general nonlinearities and a local minimality property. Acta Appl. Math. 65 (2001) 9–33. [CrossRef] [MathSciNet] [Google Scholar]
  3. F. Alessio, L. Jeanjean and P. Montecchiari, Stationary layered solutions in 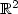Formula for a class of non autonomous Allen-Cahn equations. Calc. Var. Partial Differ. Equ. 11 (2000) 177–202. [CrossRef] [Google Scholar]
  4. F. Alessio, L. Jeanjean and P. Montecchiari, Existence of infinitely many stationary layered solutions in 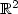Formula for a class of periodic Allen Cahn Equations. Commun. Partial Differ. Equ. 27 (2002) 1537–1574. [CrossRef] [Google Scholar]
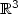  5. L. Ambrosio and X. Cabre, Entire solutions of semilinear elliptic equations in Formula and a conjecture of De Giorgi. J. Am. Math. Soc. 13 (2000) 725–739. [CrossRef] [Google Scholar]
  6. V. Bargert, On minimal laminations on the torus. Ann. Inst. H. Poincaré Anal. Nonlinéaire 6 (1989) 95–138. [Google Scholar]
  7. M.T. Barlow, R.F. Bass and C. Gui, The Liouville property and a conjecture of De Giorgi. Comm. Pure Appl. Math. 53 (2000) 1007–1038. [Google Scholar]
  8. H. Berestycki, F. Hamel and R. Monneau, One-dimensional symmetry for some bounded entire solutions of some elliptic equations. Duke Math. J. 103 (2000) 375–396. [CrossRef] [MathSciNet] [Google Scholar]
  9. E. De Giorgi, Convergence problems for functionals and operators, in Proc. Int. Meeting on Recent Methods in Nonlinear Analysis. Rome, E. De Giorgi et al. Eds. (1978). [Google Scholar]
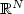  10. A. Farina, Symmetry for solutions of semilinear elliptic equations in Formula and related conjectures. Ricerche Mat. (in memory of Ennio De Giorgi) 48 (1999) 129–154. [Google Scholar]
  11. N. Ghoussoub and C. Gui, On a conjecture of De Giorgi and some related problems. Math. Ann. 311 (1998) 481–491. [CrossRef] [MathSciNet] [Google Scholar]
  12. J. Moser, Minimal solutions of variational problem on a torus. Ann. Inst. H. Poincaré Anal. NonLinéaire 3 (1986) 229–272. [Google Scholar]
  13. P.H. Rabinowitz and E. Stredulinsky, Mixed states for an Allen-Cahn type equation. Commun. Pure Appl. Math. 56 (2003) 1078–1134. [CrossRef] [MathSciNet] [Google Scholar]
  14. P.H. Rabinowitz and E. Stredulinsky, Mixed states for an Allen-Cahn type equation, II. Calc. Var. Partial Differ. Equ. 21 (2004) 157–207. [Google Scholar]
  15. P.H. Rabinowitz, Heteroclinic for reversible Hamiltonian system. Ergod. Th. Dyn. Sys. 14 (1994) 817–829. [Google Scholar]
  16. P.H. Rabinowitz, Solutions of heteroclinic type for some classes of semilinear elliptic partial differential equations. J. Math. Sci. Univ. Tokio 1 (1994) 525–550. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.