Controlled functional differential equations: approximate and exact asymptotic tracking with prescribed transient performance

¹ Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK. epr@maths.bath.ac.uk; p.townsend@bath.ac.uk
² School of Mathematics, University of Birmingham, Birmingham B15 2TT, UK. C.J.Sangwin@bham.ac.uk

Received: 25 June 2007
Revised: 26 March 2008

Abstract

A tracking problem is considered in the context of a class of multi-input, multi-output, nonlinear systems modelled by controlled functional differential equations. The class contains, as a prototype, all finite-dimensional, linear, m-input, m-output, minimum-phase systems with sign-definite “high-frequency gain". The first control objective is tracking of reference signals r by the output y of any system in : given , construct a feedback strategy which ensures that, for every r (assumed bounded with essentially bounded derivative) and every system of class , the tracking error is such that, in the case , or, in the case , 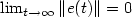. The second objective is guaranteed output transient performance: the error is required to evolve within a prescribed performance funnel (determined by a function φ). For suitably chosen functions α, ν and θ, both objectives are achieved via a control structure of the form with 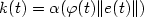, whilst maintaining boundedness of the control and gain functions u and k. In the case , the feedback strategy may be discontinuous: to accommodate this feature, a unifying framework of differential inclusions is adopted in the analysis of the general case .