Lipschitz stability in the determination of the principal part of a parabolic equation

Ganghua Yuan; Masahiro Yamamoto

doi:10.1051/cocv:2008043

All issues

Volume 15 / No 3 (July-September 2009)

ESAIM: COCV, 15 3 (2009) 525-554

Abstract

Free Access

Issue		ESAIM: COCV Volume 15, Number 3, July-September 2009


Page(s)		525 - 554
DOI		https://doi.org/10.1051/cocv:2008043
Published online		19 July 2008

ESAIM: COCV 15 (2009) 525-554

Lipschitz stability in the determination of the principal part of a parabolic equation

Ganghua Yuan¹^,2 and Masahiro Yamamoto¹

¹ Department of Mathematical Sciences, The University of Tokyo, Komaba Meguro, Tokyo, 153-8914, Japan. g_h_yuan@hotmail.com; myama@ms.u-tokyo.ac.jp
² School of Mathematics & Statistics, Northeast Normal University, Changchun, Jilin, 130024, P. R. China.

Received: 7 March 2007
Revised: 31 December 2007

Abstract

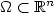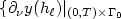Let y(h)(t,x) be one solution to $\partial_t y(t,x) - \sum_{i, j=1}^{n}\partial_{j} (a_{ij}(x)\partial_i y(t,x)) = h(t,x), \thinspace 0<t<T, \thinspace x\in \Omega$ with a non-homogeneous term h, and $y\vert_{(0,T)\times\partial\Omega} = 0$ , where $\Omega \subset \Bbb R^n$ is a bounded domain. 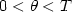We discuss an inverse problem of determining n(n+1)/2 unknown functions a_ij by $\{ \partial_{\nu}y(h_{\ell})\vert_{(0,T)\times \Gamma_0}$ , $y(h_{\ell})(\theta,\cdot)\}_{1\le \ell\le \ell_0}$ after selecting input sources $h_1, ..., h_{\ell_0}$ suitably, where $\Gamma_0$ is an arbitrary subboundary, $\partial_{\nu}$ denotes the normal derivative, $0 < \theta < T$ and $\ell_0 \in \Bbb N$ . 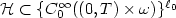In the case of $\ell_0 = (n+1)^2n/2$ , we prove the Lipschitz stability in the inverse problem if we choose $(h_1, ..., h_{\ell_0})$ from a set ${\cal H} \subset \{ C_0^{\infty} ((0,T)\times \omega)\}^{\ell_0}$ with an arbitrarily fixed subdomain 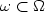$\omega \subset \Omega$ . 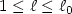Moreover we can take $\ell_0 = (n+3)n/2$ by making special choices for $h_{\ell}$ , $1 \le \ell \le \ell_0$ . The proof is based on a Carleman estimate.

Mathematics Subject Classification: 35R30 / 35K20

Key words: Inverse parabolic problem / Carleman estimate / Lipschitz stability

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.