| Issue |
ESAIM: COCV
Volume 18, Number 2, April-June 2012
|
|
|---|---|---|
| Page(s) | 383 - 400 | |
| DOI | https://doi.org/10.1051/cocv/2010102 | |
| Published online | 13 April 2011 | |
A simple proof of the characterization of functions of low Aviles Giga energy on a ball via regularity
Mathematics Department, University of Cincinnati, 2600
Clifton Ave., Cincinnati, Ohio
45221,
USA
lorentaw@uc.edu
Received:
13
April
2010
Revised:
6
September
2010
The Aviles Giga functional is a well known second order functional that forms a model for
blistering and in a certain regime liquid crystals, a related functional models thin
magnetized films. Given Lipschitz domain Ω ⊂ ℝ2 the functional
is
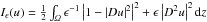 where
u belongs to the subset of functions in
where
u belongs to the subset of functions in
 whose gradient (in the
sense of trace) satisfies
Du(x)·ηx = 1
where ηx is the inward pointing unit normal
to ∂Ω at x. In [Ann. Sc. Norm. Super. Pisa Cl.
Sci. 1 (2002) 187–202] Jabin et al. characterized
a class of functions which includes all limits of sequences
whose gradient (in the
sense of trace) satisfies
Du(x)·ηx = 1
where ηx is the inward pointing unit normal
to ∂Ω at x. In [Ann. Sc. Norm. Super. Pisa Cl.
Sci. 1 (2002) 187–202] Jabin et al. characterized
a class of functions which includes all limits of sequences
 with
Iϵn(un) → 0
as ϵn → 0. A corollary to their work is that
if there exists such a sequence (un) for a
bounded domain Ω, then Ω must be a ball and (up to
change of sign)
u: = limn → ∞un = dist(·,∂Ω).
Recently [Lorent, Ann. Sc. Norm. Super. Pisa Cl. Sci. (submitted),
http://arxiv.org/abs/0902.0154v1] we provided a quantitative generalization
of this corollary over the space of convex domains using ‘compensated compactness’
inspired calculations of DeSimone et al. [Proc. Soc. Edinb. Sect.
A 131 (2001) 833–844]. In this note we use methods of regularity
theory and ODE to provide a sharper estimate and a much simpler proof for the case where
Ω = B1(0) without the requiring the trace
condition on Du.
with
Iϵn(un) → 0
as ϵn → 0. A corollary to their work is that
if there exists such a sequence (un) for a
bounded domain Ω, then Ω must be a ball and (up to
change of sign)
u: = limn → ∞un = dist(·,∂Ω).
Recently [Lorent, Ann. Sc. Norm. Super. Pisa Cl. Sci. (submitted),
http://arxiv.org/abs/0902.0154v1] we provided a quantitative generalization
of this corollary over the space of convex domains using ‘compensated compactness’
inspired calculations of DeSimone et al. [Proc. Soc. Edinb. Sect.
A 131 (2001) 833–844]. In this note we use methods of regularity
theory and ODE to provide a sharper estimate and a much simpler proof for the case where
Ω = B1(0) without the requiring the trace
condition on Du.
Mathematics Subject Classification: 49N99 / 35J30
Key words: Aviles Giga functional
© EDP Sciences, SMAI, 2011
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


