| Issue |
ESAIM: COCV
Volume 4, 1999
|
|
|---|---|---|
| Page(s) | 335 - 359 | |
| DOI | https://doi.org/10.1051/cocv:1999112 | |
| Published online | 15 August 2002 | |
Approximation of viscosity solution by morphological filters
CEREMADE,
Université de Paris Dauphine,
place de Lattre de Tassigny,
75775 Paris Cedex 16,
France; pasquig@pi.ceremade.dauphine.fr.
Received:
7
July
1998
Revised:
24
March
1999
We consider in 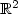 all curvature equation
all curvature equation
 where G is a nondecreasing function and
curv(u) is the curvature of the level
line passing by x. These equations are invariant with respect
to any contrast change u → g(u), with g nondecreasing.
Consider the contrast invariant operator
where G is a nondecreasing function and
curv(u) is the curvature of the level
line passing by x. These equations are invariant with respect
to any contrast change u → g(u), with g nondecreasing.
Consider the contrast invariant operator
 .
A Matheron theorem asserts that all contrast invariant operator
T can be put in a form
.
A Matheron theorem asserts that all contrast invariant operator
T can be put in a form
 .
We show the asymptotic equivalence of both formulations.
More precisely, we show that all curvature equations can be obtained as
the iteration of Matheron operators
.
We show the asymptotic equivalence of both formulations.
More precisely, we show that all curvature equations can be obtained as
the iteration of Matheron operators  where
h → 0 and n → ∞ with nh=t.
where
h → 0 and n → ∞ with nh=t.
Résumé
Nous considérons dans 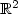 les équations de courbure
les équations de courbure
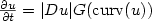 où G est une fonction croissante
et curv(u) représente la courbure
de la ligne de niveau passant par le point x. Ces
équations sont invariantes pour tout changement
de contraste u → g(u), avec g croissante.
D'autre part, Matheron a prouvé
que tout opérateur invariant par changement de contraste
où G est une fonction croissante
et curv(u) représente la courbure
de la ligne de niveau passant par le point x. Ces
équations sont invariantes pour tout changement
de contraste u → g(u), avec g croissante.
D'autre part, Matheron a prouvé
que tout opérateur invariant par changement de contraste
 peut s'exprimer comme un schéma inf-sup
peut s'exprimer comme un schéma inf-sup  . Nous démontrons
l'équivalence asymtotique
de ces deux approches. Plus précisément, nous prouvons que
la solution de viscosité de toute
équation de courbure est la limite d'opérateurs de Matheron
itérés
. Nous démontrons
l'équivalence asymtotique
de ces deux approches. Plus précisément, nous prouvons que
la solution de viscosité de toute
équation de courbure est la limite d'opérateurs de Matheron
itérés 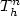 lorsque h → 0
et n → ∞ avec nh=t.
lorsque h → 0
et n → ∞ avec nh=t.
Mathematics Subject Classification: 65N12 / 35K65 / 53C21 / 76T05
Key words: Viscosity solutions / inf-sup scheme / morphological filter.
© EDP Sciences, SMAI, 1999
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


