EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 7 (2002) ESAIM: COCV, 7 (2002) 97-133 References
Free Access
Issue
ESAIM: COCV
Volume 7, 2002
Page(s) 97 - 133
DOI https://doi.org/10.1051/cocv:2002005
Published online 15 September 2002
  1. F. Ancona and A. Bressan, Patchy vector fields and asymptotic stabilization. ESAIM: COCV 4 (1999) 445-471. [CrossRef] [EDP Sciences] [Google Scholar]
  2. N.N. Barabanova and A.I. Subbotin, On continuous evasion strategies in game theoretic problems on the encounter of motions. Prikl. Mat. Mekh. 34 (1970) 796-803. [Google Scholar]
  3. N.N. Barabanova and A.I. Subbotin, On classes of strategies in differential games of evasion. Prikl. Mat. Mekh. 35 (1971) 385-392. [Google Scholar]
  4. M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations. Birkhäuser, Boston (1997). [Google Scholar]
  5. L.D. Berkovitz, Optimal feedback controls. SIAM J. Control Optim. 27 (1989) 991-1006. [Google Scholar]
  6. P. Cannarsa and H. Frankowska, Some characterizations of optimal trajectories in control theory. SIAM J. Control Optim. 29 (1991) 1322-1347. [CrossRef] [MathSciNet] [Google Scholar]
  7. I. Capuzzo-Dolcetta and P.L. Lions, Hamilton-Jacobi equations with state constraints. Trans. Amer. Math. Soc. 318 (1990) 643-683. [Google Scholar]
  8. F.H. Clarke, Optimization and Nonsmooth Analysis. Wiley-Interscience, New York (1983). Republished as Vol. 5 of Classics in Appl. Math. SIAM, Philadelphia (1990). [Google Scholar]
  9. F.H. Clarke, Methods of Dynamic and Nonsmooth Optimization, Vol. 57 of CBMS-NSF Regional Conference Series in Applied Mathematics. SIAM, Philadelphia (1989). [Google Scholar]
  10. F.H. Clarke, Yu.S. Ledyaev, L. Rifford and R.J. Stern, Feedback stabilization and Lyapunov functions. SIAM J. Control Optim. 39 (2000) 25-48. [CrossRef] [MathSciNet] [Google Scholar]
  11. F.H. Clarke, Yu.S. Ledyaev, E.D. Sontag and A.I. Subbotin, Asymptotic controllability implies control feedback stabilization. IEEE Trans. Automat. Control 42 (1997) 1394. [CrossRef] [MathSciNet] [Google Scholar]
  12. F.H. Clarke, Yu.S. Ledyaev and R.J. Stern, Proximal analysis and control feedback construction. Proc. Steklov Inst. Math. 226 (2000) 1-20. [Google Scholar]
  13. F.H. Clarke, Yu.S. Ledyaev, R.J. Stern and P.R. Wolenski, Qualitative properties of trajectories of control systems: A survey. J. Dynam. Control Systems 1 (1995) 1-48. [CrossRef] [MathSciNet] [Google Scholar]
  14. F.H. Clarke, Yu.S. Ledyaev and A.I. Subbotin, Universal feedback strategies for differential games of pursuit. SIAM J. Control Optim. 35 (1997) 552-561. [CrossRef] [MathSciNet] [Google Scholar]
  15. F.H. Clarke, Yu.S. Ledyaev and A.I. Subbotin, Universal positional control. Proc. Steklov Inst. Math. 224 (1999) 165-186. Preliminary version: Preprint CRM-2386. Univ. de Montréal (1994). [Google Scholar]
  16. F.H. Clarke, Yu.S. Ledyaev and R.J. Stern, Complements, approximations, smoothings and invariance properties. J. Convex Anal. 4 (1997) 189-219. [MathSciNet] [Google Scholar]
  17. F.H. Clarke, Yu.S. Ledyaev, R.J. Stern and P.R. Wolenski, Nonsmooth Analysis and Control Theory. Springer-Verlag, New York, Grad. Texts in Math. 178 (1998). [Google Scholar]
  18. F.H. Clarke, R.J. Stern and P.R. Wolenski, Proximal smoothness and the lower-C2 property. J. Convex Anal. 2 (1995) 117-145. [MathSciNet] [Google Scholar]
  19. F. Forcellini and F. Rampazzo, On nonconvex differential inclusions whose state is constrained in the closure of an open set. Applications to dynamic programming. Differential and Integral Equations 12 (1999) 471-497. [MathSciNet] [Google Scholar]
  20. H. Frankowska and F. Rampazzo, Filippov's and Filippov-Wazewski's theorems on closed domains. J. Differential Equations 161 (2000) 449-478. [CrossRef] [MathSciNet] [Google Scholar]
  21. G.G. Garnysheva and A.I. Subbotin, Suboptimal universal strategies in a game-theoretic time-optimality problem. Prikl. Mat. Mekh. 59 (1995) 707-713. [Google Scholar]
  22. J.-B. Hiriart-Urruty, New concepts in nondifferentiable programming. Bull. Soc. Math. France 60 (1979) 57-85. [Google Scholar]
  23. H. Ishii and S. Koike, On ε-optimal controls for state constraint problems. Ann. Inst. H. Poincaré Anal. Linéaire 17 (2000) 473-502. [Google Scholar]
  24. N.N. Krasovskii, Differential games. Approximate and formal models. Mat. Sb. (N.S.) 107 (1978) 541-571. [MathSciNet] [Google Scholar]
  25. N.N. Krasovskii, Extremal aiming and extremal displacement in a game-theoretical control. Problems Control Inform. Theory 13 (1984) 287-302. [Google Scholar]
  26. N.N. Krasovskii, Control of dynamical systems. Nauka, Moscow (1985). [Google Scholar]
  27. N.N. Krasovskii and A.I. Subbotin, Positional Differential Games. Nauka, Moscow (1974). French translation: Jeux Différentielles. Mir, Moscou (1979). [Google Scholar]
  28. N.N. Krasovskii and A.I. Subbotin, Game-Theoretical Control Problems. Springer-Verlag, New York (1988). [Google Scholar]
  29. P. Loewen, Optimal Control via Nonsmooth Analysis. CRM Proc. Lecture Notes Amer. Math. Soc. 2 (1993). [Google Scholar]
  30. S. Nobakhtian and R.J. Stern, Universal near-optimal control feedbacks. J. Optim. Theory Appl. 107 (2000) 89-123. [CrossRef] [MathSciNet] [Google Scholar]
  31. L. Rifford, Problèmes de Stabilisation en Théorie du Contrôle, Doctoral Thesis. Univ. Claude Bernard Lyon 1 (2000). [Google Scholar]
  32. L. Rifford, Stabilisation des systèmes globalement asymptotiquement commandables. C. R. Acad. Sci. Paris 330 (2000) 211-216. [Google Scholar]
  33. L. Rifford, Existence of Lipschitz and semiconcave control-Lyapunov functions. SIAM J. Control Optim. (to appear). [Google Scholar]
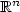  34. R.T. Rockafellar, Clarke's tangent cones and boundaries of closed sets in Formula . Nonlinear Anal. 3 (1979) 145-154. [CrossRef] [MathSciNet] [Google Scholar]
  35. R.T. Rockafellar, Favorable classes of Lipschitz continuous functions in subgradient optimization, in Nondifferentiable Optimization, edited by E. Nurminski. Permagon Press, New York (1982). [Google Scholar]
  36. J.D.L. Rowland and R.B. Vinter, Construction of optimal control feedback controls. Systems Control Lett. 16 (1991) 357-357. [Google Scholar]
  37. M. Soner, Optimal control problems with state-space constraints I. SIAM J. Control Optim. 24 (1986) 551-561. [Google Scholar]
  38. E.D. Sontag, Mathematical Control Theory, 2nd Ed.. Springer-Verlag, New York, Texts in Appl. Math. 6 (1998). [Google Scholar]
  39. E.D. Sontag, Clock and insensitivity to small measurement errors. ESAIM: COCV 4 (1999) 537-557. [CrossRef] [EDP Sciences] [Google Scholar]
  40. A.I. Subbotin, Generalized Solutions of First Order PDE's. Birkhäuser, Boston (1995). [Google Scholar]
  41. N.N. Subbotina, Universal optimal strategies in positional differential games. Differential Equations 19 (1983) 1377-1382. [Google Scholar]
  42. N.N. Subbotina, The maximum principle and the superdifferential of the value function. Problems Control Inform. Theory 18 (1989) 151-160. [Google Scholar]
  43. N.N. Subbotina, On structure of optimal feedbacks to control problems, Preprints of the eleventh IFAC International Workshop, Control Applications of Optimization, edited by V. Zakharov (2000). [Google Scholar]
  44. R.B. Vinter, Optimal Control. Birkhäuser, Boston (2000). [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.